Módulo 3
Isabel W. Vásquez M.
Clase 1
Gráficas, funciones, magnitudes escalares y vectoriales
Queridos alumnos les doy la más cordial bienvenida a esta su primera clase del módulo N°3. que pertenece a gráficas, funciones, magnitudes escalares y vectoriales, en el cual se analizará la importancia de las representaciones gráficas para la descripción de un conjunto de datos, producto de una medición, se identificará las diferencias entre las magnitudes escalares y las magnitudes vectoriales y se utilizara métodos gráficos y analíticos para la suma y resta de vectores.
Gráficas y funciones
Para empezar este módulo es fundamental que conozcamos de antemano que es una grafica. Una gráfica es una representación de datos numéricos mediante puntos y líneas que son dibujados generalmente en un plano cartesiano. Su uso permite analizar el comportamiento de un proceso o un conjunto de elementos. A continuación se presenta algunos ejemplos de ellas:
Ahora discutiremos algunos tipos importantes de funciones y observaremos sus gráficas. Pon atención a la forma que tienen las gráficas de estas funciones.
Función lineal
El gráfico lineal se compone de una serie de datos representados por puntos, unidos por segmentos lineales. Mediante este gráfico se puede comprobar rápidamente el cambio de tenencia de los datos. La función lineal se define por la ecuación y = mx + b, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.
- La variable dependiente es aquella que sólo se puedo medir. Esta variable se coloca en el eje vertical (eje y)
- variable independiente es aquella que se puede controlar. Es decir, el experimentador establece los valores que tendrá, esta se coloca en el eje horizontal (eje x)
Los elementos para construir una grafica son:
- Título de la grafica en el centro de la parte superior.
- Nombre asignado a los ejes coordenados (x, y), junto con sus unidades de medición entre paréntesis.
- Escala para cada uno de los ejes. Esta se coloca debajo del título de la gráfica.
- Los pares ordenados de datos posicionados sobre el plato cartesiano lo más exacto posible.
- Línea continua que uno los puntos colocados sobre el plano cartesiano.
La siguiente imagen muestra los elementos de una gráfica.
Les invito a ver el siguiente Slideshare en donde se muestra un ejemplo de gráfica de función lineal, con sus variables dependiente e independiente ordenadas en una tabla de datos, y explica como determinar la pendiente, los puntos de intersección y la ecuación del gráfico.
Función potencial
Magnitudes escalares y vectoriales
- Las magnitudes escalares son aquellas que quedan completamente definidas por un número y las unidades utilizadas para su medida. Las magnitudes escalares están representadas por el ente matemático más simple, por un número. Podemos decir que poseen un módulo pero carecen de dirección.
- Las magnitudes vectoriales son aquellas que quedan caracterizadas por una cantidad (intensidad o módulo), una dirección y un sentido y se representan por vectores. Ejemplos de estas magnitudes son: la velocidad, la aceleración, la fuerza, el campo eléctrico, intensidad luminosa, etc.
Suma y resta de vectores
Método analítico
En Física es común encontrarse una suma de cantidades vectoriales, y aunque podemos recurrir a diversos métodos como el del triángulo, del polígono o el paralelogramo, es importante tener en cuenta que la forma analítica nos conducirá a un resultado más exacto. Ahora veamos que necesitamos para comprender por completo el método analítico.
Les invito a ver el siguiente video sobre suma y resta de vectores escritos por componentes, en donde se da una explicación clara sobre el tema.
Suma de Vectores: Método Gráfico
- El método del paralelogramo permite sumar dos vectores de manera sencilla. Consiste en colocar los dos vectores, con su magnitud a escala, dirección y sentido originales, en el origen, de manera que los dos vectores inicien en el mismo punto.
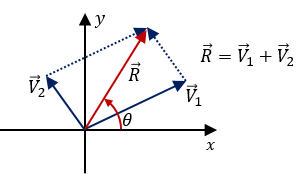
- El método gráfico también conocido como el método del polígono consiste en dibujar los vectores como segmentos dirigidos con la dirección y sentido real de estos.
RESTA DE VECTORES: Método Gráfico
Método del paralelogramo
- Determinar el vector opuesto a v, que es –v, tal como se describió antes para el método del triángulo.
- Trasladar cuidadosamente los vectores u y –v de tal manera que sus orígenes coincidan.
- Ahora se trazan líneas paralelas segmentadas que parten desde los extremos de cada vector. La figura que se forma es un paralelogramo y en casos especiales en que los vectores sean perpendiculares, resulta un rectángulo o un cuadrado.
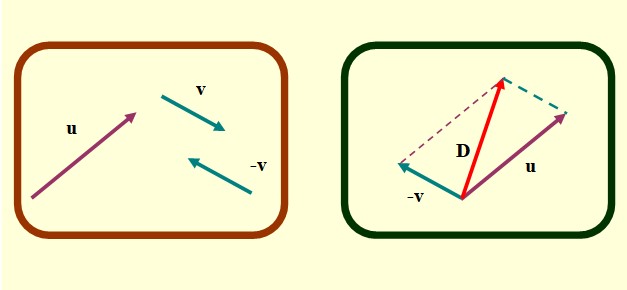 Fuente: F. Zapata.
Fuente: F. Zapata.
Bibliografía
- Álvarez Areces, Santiago; Fernández Flórez, Manuel (6 de 1990). Matemáticas, área formativa común, 1 FP, 1 grado (1 edición). Editorial Everest, S.A. p. 432.
- Larrauri Pacheco, Agustín (3 de 1997). Matemáticas, FP 1 (10 edición). Larrauri Editorial, S.A. p. 496.
- Alvarenga, B y Máximo, A, (1990). Física General con Experimentos Sencillos. Editorial Harla. México.
- Blatt, F. (1991). Fundamentos de Física. Editorial Mc Graw Hill. México.
- Bueche, F.(1990). Fundamentos de Física. Editorial Mc Graw Hill. México.
- Tippens, P. (1990). Física, Conceptos y Aplicaciones. Editorial Mc Graw Hill. México.
- Monsó Ferré, Fernando (2009). Física y Química 3º ESO. Barcelona (España): edebé. p. (1998).
Actividades
Elaboración de un mapa conceptual





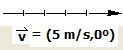


Comentarios
Publicar un comentario